Reversed-Z Rendering in OpenGL

20 Sep 2021

By default the OpenGL 3D normalized device coordinates (NDC) are between -1 and +1. x is from left to right and y is from bottom to top of the screen while the z-axis is pointing into the screen.

Usually the 3D camera coordinates of the object are mapped such that near coordinates are mapped to -1 and far values are mapped to +1. The near and far plane define the nearest and farthest point visualized by the rendering pipeline.

The absolute accuracy of floating point values is highest when the values are near zero. This leads to the depth accuracy to be highest somewhere between the near and far plane which is suboptimal.

A better solution is to map near coordinates to 1 and far coordinates to 0. In this case the higher precision near zero is used to compensate for the large range of distances covered towards the far plane.

Fortunately OpenGL 4.5 provides a way to perform reversed-z rendering:

• set glDepthFunc to GL_GREATER or GL_GEQUAL
• set glClipControl to GL_LOWER_LEFT and GL_ZERO_TO_ONE
• set glClearDepth to 0.0
• use a suitable projection matrix

Let x, y, z, 1 be the homogeneous coordinate of the 3D point and x’, y’, z’, w’ the homogeneous NDC. Normally the 3D point uses a right-handed coordinate system where the z-axis points out of the screen.

This means that x and y are projected using negative z, i.e. w’ = -z.

The camera projection equations are x’/w’ = fw x/-z and y’/w’ = fh y/-z.

Substituting w’ = -z we get x’ = fw x and y’ = fh y.

Setting z’ = a + b z we get the following matrix equation:

When z = -near, we want z’/w’ = 1.

When z = -far, we want z’/w’ = 0.

For z = -near we get: z’ = w’ => a + b z = -z => a - b near = near.

For z = -far we get: z’ = 0 => a + b z = 0 => a - b far = 0 <=> b = a / far.

Substituting b we get: a - a near / far = near <=> a = near far / (far - near)

This means b = a / far = near / (far - near).

I.e. we get:

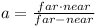
and

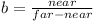
Finally we set fw = 1 / tan(fov / 2) where fov is the horizontal field of view angle (e.g. 60 degrees in radians).

fh then needs to be chosen such that fh / fw = w / h, where w and h are the width and height of the screen.